basis.hpp File Reference

#include <boost/multi_array.hpp>
#include <mesh.hpp>
#include <iostream>
#include <polynomialspacedimension.hpp>
#include <quadraturerule.hpp>

Include dependency graph for basis.hpp:

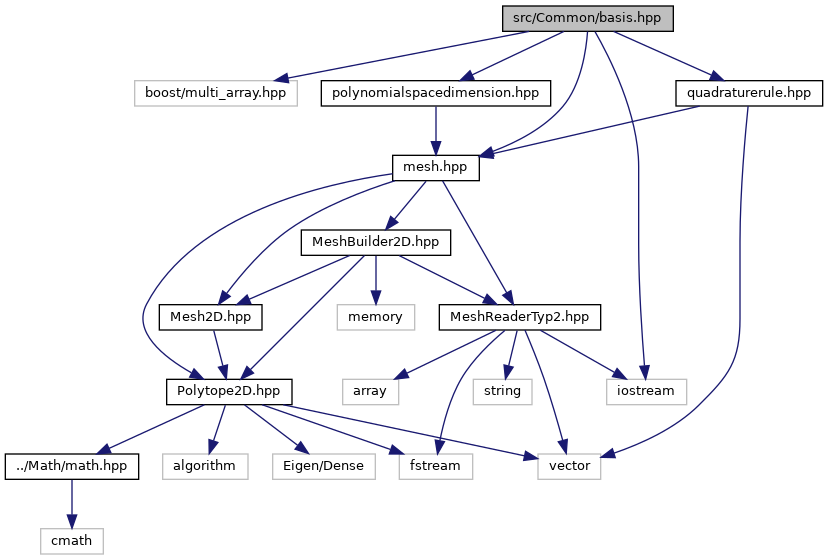
This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Classes
struct	HArDCore2D::MonomialPowers< GeometricSupport >
	Compute vectors listing the powers of monomial basis functions (for a cell, only this specialization is relevant) up to a certain degree. More...
struct	HArDCore2D::MonomialPowers< Cell >
struct	HArDCore2D::MatrixGradient< N >
	Structure to store the gradient of a matrix-valued function. More...
class	HArDCore2D::MonomialScalarBasisCell
	Scalar monomial basis on a cell. More...
class	HArDCore2D::MonomialScalarBasisEdge
	Scalar monomial basis on an edge. More...
class	HArDCore2D::Family< BasisType >
class	HArDCore2D::TensorizedVectorFamily< ScalarFamilyType, N >
	Vector family obtained by tensorization of a scalar family. More...
class	HArDCore2D::MatrixFamily< ScalarFamilyType, N >
	Matrix family obtained from a scalar family. More...
class	HArDCore2D::TangentFamily< ScalarFamilyType >
	Vector family for polynomial functions that are tangent to an edge (determined by the generator) More...
class	HArDCore2D::ShiftedBasis< BasisType >
	Generate a basis where the function indices are shifted. More...
class	HArDCore2D::RestrictedBasis< BasisType >
	Generate a basis restricted to the first "dimension" functions. More...
class	HArDCore2D::GradientBasis< BasisType >
	Basis for the space of gradients of polynomials. More...
class	HArDCore2D::CurlBasis< BasisType >
	Basis for the space of curls (vectorial rot) of polynomials. More...
class	HArDCore2D::DivergenceBasis< BasisType >
	Basis (or rather family) of divergence of an existing basis. More...
class	HArDCore2D::RotorBasis< BasisType >
	Basis (or rather family) of scalar rotor of an existing basis. More...
class	HArDCore2D::HessianBasis< BasisType >
	Basis for the space of Hessians of polynomials. More...
class	HArDCore2D::RolyComplBasisCell
	Basis for the complement R^{c,k}(T) in P^k(T)^2 of the range of the vectorial rotational on a face. More...
class	HArDCore2D::GolyComplBasisCell
	Basis for the complement G^{c,k}(T) in P^k(F)^2 of the range of the gradient on a face. More...
class	HArDCore2D::HolyComplBasisCell
	Basis for the complement H^{c,k}(T) in P^k(T)^{2x2} of the range of the Hessian on a face. More...
struct	HArDCore2D::detail::basis_evaluation_traits< BasisType, BasisFunction >
	Basis evaluation traits. Only specialization of 'BasisFunction' (=Function, Gradient, Curl, Divergence, or Rotor) are relevant, and determines what kind of value we want to evaluate. More...
struct	HArDCore2D::detail::basis_evaluation_traits< BasisType, Function >
struct	HArDCore2D::detail::basis_evaluation_traits< BasisType, Gradient >
struct	HArDCore2D::detail::basis_evaluation_traits< BasisType, SymmetricGradient >
struct	HArDCore2D::detail::basis_evaluation_traits< BasisType, SkewsymmetricGradient >
struct	HArDCore2D::detail::basis_evaluation_traits< BasisType, Curl >
struct	HArDCore2D::detail::basis_evaluation_traits< BasisType, Divergence >
struct	HArDCore2D::detail::basis_evaluation_traits< BasisType, Rotor >
struct	HArDCore2D::detail::basis_evaluation_traits< BasisType, Hessian >
struct	HArDCore2D::detail::basis_evaluation_traits< TensorizedVectorFamily< ScalarBasisType, N >, Function >
struct	HArDCore2D::detail::basis_evaluation_traits< TensorizedVectorFamily< ScalarBasisType, N >, Gradient >
struct	HArDCore2D::detail::basis_evaluation_traits< TensorizedVectorFamily< ScalarBasisType, N >, SymmetricGradient >
struct	HArDCore2D::detail::basis_evaluation_traits< TensorizedVectorFamily< ScalarBasisType, N >, SkewsymmetricGradient >
struct	HArDCore2D::detail::basis_evaluation_traits< TensorizedVectorFamily< ScalarBasisType, N >, Curl >
struct	HArDCore2D::detail::basis_evaluation_traits< TensorizedVectorFamily< ScalarBasisType, N >, Divergence >
struct	HArDCore2D::detail::basis_evaluation_traits< TensorizedVectorFamily< ScalarBasisType, N >, Rotor >
struct	HArDCore2D::detail::basis_evaluation_traits< MatrixFamily< ScalarBasisType, N >, Function >
struct	HArDCore2D::detail::basis_evaluation_traits< MatrixFamily< ScalarBasisType, N >, Divergence >
struct	HArDCore2D::detail::basis_evaluation_traits< MatrixFamily< ScalarBasisType, N >, Gradient >
struct	HArDCore2D::evaluate_quad< BasisFunction >
	Evaluate a basis at quadrature nodes. 'BasisFunction' (=Function, Gradient, Curl, Divergence, or Rotor) determines what kind of value we want to evaluate. More...
struct	HArDCore2D::DecomposePoly< BasisType >
	Structure to decompose a set of polynomials on a basis on an edge or a cell. More...

Namespaces
namespace	HArDCore2D
namespace	HArDCore2D::detail

Typedefs
typedef Eigen::Matrix2d	HArDCore2D::MatrixRd
typedef Eigen::Vector2d	HArDCore2D::VectorRd
typedef Eigen::Vector2i	HArDCore2D::VectorZd
template<typename T >
using	HArDCore2D::BasisQuad = boost::multi_array< T, 2 >
	type for a family of basis functions evaluated on quadrature nodes
template<typename T >
using	HArDCore2D::FType = std::function< T(const VectorRd &)>
	type for function of point. T is the type of value of the function

Enumerations
enum	HArDCore2D::TensorRankE { HArDCore2D::Scalar = 0 , HArDCore2D::Vector = 1 , HArDCore2D::Matrix = 2 }
enum	HArDCore2D::BasisFunctionE {   HArDCore2D::Function , HArDCore2D::Gradient , HArDCore2D::SymmetricGradient , HArDCore2D::SkewsymmetricGradient ,   HArDCore2D::Curl , HArDCore2D::Divergence , HArDCore2D::Rotor , HArDCore2D::Hessian }

Functions
template<size_t N>
MatrixGradient< N >	HArDCore2D::operator* (double scalar, MatrixGradient< N > const &G)
	Multiplication of a MatrixGradient from the left (non-member function to be able to multiply from the left)
template<typename outValue , typename inValue , typename FunctionType >
boost::multi_array< outValue, 2 >	HArDCore2D::transform_values_quad (const boost::multi_array< inValue, 2 > &B_quad, const FunctionType &F)
	Takes an array B_quad of values at quadrature nodes and applies the function F to all of them. F must take inValue and return outValue. The function must be called with outValue as template argument: transform_values_quad<outValue>(...)
template<typename ScalarBasisType , size_t N>
Family< TensorizedVectorFamily< ScalarBasisType, N > >	HArDCore2D::GenericTensorization (const ScalarBasisType &B, const std::vector< Eigen::VectorXd > &v)
	From a scalar family B=(B_1..B_r) and vectors (v_1..v_k) in R^N, constructs a "Family" of "TensorizedVectorFamily" (built on B, of size N) that represents the family (B_1v_1..B_rv_1 B_1v_2...B_rv_2... B_1v_k..B_rv_k).
template<typename ScalarBasisType , size_t N>
Family< MatrixFamily< ScalarBasisType, N > >	HArDCore2D::IsotropicMatrixFamily (const ScalarBasisType &B)
	From a scalar family B, constructs a "Family" of "MatrixFamily" (built on B, of size NxN) that represents the family B Id on the MatrixFamily.
template<typename T >
Eigen::MatrixXd	HArDCore2D::gram_schmidt (boost::multi_array< T, 2 > &basis_eval, const std::function< double(size_t, size_t)> &inner_product)
double	HArDCore2D::scalar_product (const double &x, const double &y)
	Scalar product between two reals.
double	HArDCore2D::scalar_product (const VectorRd &x, const VectorRd &y)
	Scalar product between two vectors.
template<int N>
double	HArDCore2D::scalar_product (const Eigen::Matrix< double, N, N > &x, const Eigen::Matrix< double, N, N > &y)
	Scalar product between two matrices.
template<typename Value >
boost::multi_array< double, 2 >	HArDCore2D::scalar_product (const boost::multi_array< Value, 2 > &basis_quad, const Value &v)
	This overloading of the scalar_product function computes the scalar product between an evaluation of a basis and a constant value; both basis values and constant value must be of type Value.
template<typename Value >
boost::multi_array< double, 2 >	HArDCore2D::scalar_product (const boost::multi_array< Value, 2 > &basis_quad, const std::vector< Value > &v)
	This overloading of the scalar_product function computes the scalar product between an evaluation of a basis and a field that varies on the quadrature nodes; both basis values and constant value must be of type Value.
boost::multi_array< VectorRd, 2 >	HArDCore2D::matrix_vector_product (const boost::multi_array< MatrixRd, 2 > &basis_quad, const std::vector< VectorRd > &v_quad)
	Take the product of a matrix-valued basis with a vector.
boost::multi_array< VectorRd, 2 >	HArDCore2D::matrix_vector_product (const std::vector< MatrixRd > &m_quad, const boost::multi_array< VectorRd, 2 > &basis_quad)
	Take the product of a matrix with a vector-valued basis.
boost::multi_array< VectorRd, 2 >	HArDCore2D::vector_matrix_product (const std::vector< VectorRd > &v_quad, const boost::multi_array< MatrixRd, 2 > &basis_quad)
	Take the product of (the transposed of) a vector with a matrix-valued basis.
template<typename BasisType >
Family< BasisType >	HArDCore2D::l2_orthonormalize (const BasisType &basis, const QuadratureRule &qr, boost::multi_array< typename BasisType::FunctionValue, 2 > &basis_quad)
	\(L^2\)-orthonormalization: simply consists in using gram_schmidt() with the specific l2 inner product
template<typename BasisType >
Family< BasisType >	HArDCore2D::l2_orthonormalize (const BasisType &basis, const Eigen::MatrixXd &GM)
	\(L^2\)-orthonormalization: when the Gram Matrix is passed, we use Cholesky.
template<typename FunctionValue >
Eigen::MatrixXd	HArDCore2D::compute_gram_matrix (const boost::multi_array< FunctionValue, 2 > &B1, const boost::multi_array< FunctionValue, 2 > &B2, const QuadratureRule &qr, const size_t nrows, const size_t ncols, const std::string sym="nonsym")
	Compute the Gram-like matrix given the evaluation of two families of functions at quadrature nodes. This templated function is very generic, and thus not the most efficient. More efficient overloads are provided for double- or Vector2d-valued families.
template<typename FunctionValue >
Eigen::MatrixXd	HArDCore2D::compute_gram_matrix (const boost::multi_array< FunctionValue, 2 > &B1, const boost::multi_array< FunctionValue, 2 > &B2, const QuadratureRule &qr, const std::string sym="nonsym")
	Compute the Gram-like matrix given the evaluation of two families of functions at quadrature nodes. This version calls the generic one with nrows = nb of elements in family B1 and ncols = nb of elements in family B2.
template<typename FunctionValue >
Eigen::MatrixXd	HArDCore2D::compute_gram_matrix (const boost::multi_array< FunctionValue, 2 > &B, const QuadratureRule &qr)
	Compute the Gram matrix given the evaluation of one family of functions at quadrature nodes. Consists in calling the generic templated version with B1=B2.
Eigen::MatrixXd	HArDCore2D::compute_gram_matrix (const boost::multi_array< VectorRd, 2 > &B1, const boost::multi_array< double, 2 > &B2, const QuadratureRule &qr)
	Compute the Gram-like matrix given a family of vector-valued and one of scalar-valued functions by tensorizing the latter.
Eigen::MatrixXd	HArDCore2D::compute_gram_matrix (const boost::multi_array< double, 2 > &B1, const boost::multi_array< double, 2 > &B2, const QuadratureRule &qr, const size_t nrows, const size_t ncols, const std::string sym="nonsym")
	Compute the Gram-like matrix given the evaluation of two families of functions at quadrature nodes. This version is an overload for double-valued families, more efficient than the generic templated version.
Eigen::MatrixXd	HArDCore2D::compute_gram_matrix (const boost::multi_array< double, 2 > &B1, const boost::multi_array< double, 2 > &B2, const QuadratureRule &qr, const std::string sym="nonsym")
	Compute the Gram-like matrix given the evaluation of two families of functions at quadrature nodes. Consists in calling the double-valued version with nrows = nb of elements in B1, ncols = nb of elements in B2.
Eigen::MatrixXd	HArDCore2D::compute_gram_matrix (const boost::multi_array< VectorRd, 2 > &B1, const boost::multi_array< VectorRd, 2 > &B2, const QuadratureRule &qr, const size_t nrows, const size_t ncols, const std::string sym="nonsym")
	Compute the Gram-like matrix given the evaluation of two families of functions at quadrature nodes. This version is an overload for Vector2d-valued families, more efficient than the generic templated version.
Eigen::MatrixXd	HArDCore2D::compute_gram_matrix (const boost::multi_array< VectorRd, 2 > &B1, const boost::multi_array< VectorRd, 2 > &B2, const QuadratureRule &qr, const std::string sym="nonsym")
	Compute the Gram-like matrix given the evaluation of two families of functions at quadrature nodes. Consists in calling the Vector2d-valued version with nrows = nb of elements in B1, ncols = nb of elements in B2.
template<typename ScalarFamilyType , size_t N>
Eigen::MatrixXd	HArDCore2D::compute_gram_matrix (const MatrixFamily< ScalarFamilyType, N > &MatFam, const boost::multi_array< double, 2 > &scalar_family_quad, const QuadratureRule &qr)
	Compute the Gram-like matrix for a MatrixFamily. This overload is more efficient than the generic function as it only computes the gram matrix of the underlying scalar family, and then creates the bloc-diagonal gram matrix of the MatrixFamily (which is indeed bloc diagonal given the choice of m_E elements in this class).
template<typename T >
Eigen::VectorXd	HArDCore2D::integrate (const FType< T > &f, const BasisQuad< T > &B, const QuadratureRule &qr, size_t n_rows=0)
	Compute the integral of a given function against all functions from a family.
template<typename T , typename U >
Eigen::MatrixXd	HArDCore2D::compute_weighted_gram_matrix (const FType< U > &f, const BasisQuad< T > &B1, const BasisQuad< T > &B2, const QuadratureRule &qr, size_t n_rows=0, size_t n_cols=0, const std::string sym="nonsym")
	Computes the Gram-like matrix of integrals (f phi_i, phi_j)
template<typename T , typename U >
Eigen::MatrixXd	HArDCore2D::compute_weighted_gram_matrix (const FType< U > &f, const BasisQuad< T > &B1, const BasisQuad< T > &B2, const QuadratureRule &qr, const std::string sym)
	Computes the Gram-like matrix of integrals (f phi_i, phi_j)
Eigen::MatrixXd	HArDCore2D::compute_weighted_gram_matrix (const FType< VectorRd > &f, const BasisQuad< VectorRd > &B1, const BasisQuad< double > &B2, const QuadratureRule &qr, size_t n_rows=0, size_t n_cols=0)
	Computes the Gram-like matrix of integrals (f dot phi_i, phi_j)
Eigen::MatrixXd	HArDCore2D::compute_weighted_gram_matrix (const FType< VectorRd > &f, const BasisQuad< double > &B1, const BasisQuad< VectorRd > &B2, const QuadratureRule &qr, size_t n_rows=0, size_t n_cols=0)
	Computes the Gram-like matrix of integrals (phi_i, f dot phi_j)
template<typename Value >
Eigen::MatrixXd	HArDCore2D::compute_closure_matrix (const boost::multi_array< Value, 2 > &f_quad, const boost::multi_array< Value, 2 > &g_quad, const QuadratureRule &qr_f, const QuadratureRule &qr_g)
	Computes closure equation matrices, from evaluations at quadrature nodes. For two families of functions \((f_i)\) and \((g_j)\) with values in some space E, this routine computes the matrix \((\int f_i)\cdot(\int g_j)\) where \(\cdot\) is the dot product in E.
template<typename Value >
Eigen::MatrixXd	HArDCore2D::compute_closure_matrix (const boost::multi_array< Value, 2 > &f_quad, const boost::multi_array< Value, 2 > &g_quad, const QuadratureRule &qr)
	Computes closure equation matrices. Overload of the previous one when qr_f=qr_g.
template<typename Value >
Eigen::MatrixXd	HArDCore2D::compute_closure_matrix (const boost::multi_array< Value, 2 > &f_quad, const QuadratureRule &qr)
	Computes closure equation matrices. Overload of the previous one when f=g.
template<typename BasisType >
Eigen::VectorXd	HArDCore2D::l2_projection (const std::function< typename BasisType::FunctionValue(const VectorRd &)> &f, const BasisType &basis, QuadratureRule &quad, const boost::multi_array< typename BasisType::FunctionValue, 2 > &basis_quad, const Eigen::MatrixXd &mass_basis=Eigen::MatrixXd::Zero(1, 1))
	Compute the L2-projection of a function.

Variables
constexpr int	HArDCore2D::dimspace = 2
	Dimension, and generic types for vector in correct dimension (makes it easier to translate a code between 2D and 3D)
static std::function< Eigen::MatrixXd(const Eigen::MatrixXd &)>	HArDCore2D::symmetrise_matrix = [](const Eigen::MatrixXd & x)->Eigen::MatrixXd { return 0.5*(x+x.transpose());}
	Function to symmetrise a matrix (useful together with transform_values_quad)
static std::function< Eigen::MatrixXd(const Eigen::MatrixXd &)>	HArDCore2D::skew_symmetrise_matrix = [](const Eigen::MatrixXd & x)->Eigen::MatrixXd { return 0.5*(x-x.transpose());}
	Function to skew-symmetrise a matrix (useful together with transform_values_quad)